UKUK USUSIndiaIndia

Teaching by Asking!

Parents Students Tutors Teachers Safe Ai Knowledge Bank Survey Results Blog
Join Us
UKUK USUSIndiaIndia
Join Us
KS1 (Age 5-7)KS2 (Age 7-11)11 Plus (Age 7-11)KS3 (Age 11-14)GCSE (Age 14-17)PSHEA.I.ESLSpanishSpecialistGames
Lucy
Ask the AI Tutor
Need help with Level 7-8 Shapes - Pythagoras 02? Ask our AI Tutor!
Lucy AI Tutor - Lucy
Connecting with Tutor...
Please wait while we establish connection
Lucy
Hi! I'm Lucy, your AI tutor. How can I help you with Level 7-8 Shapes - Pythagoras 02 today?
now
0/50 words
  1. Home
  2. KS3
  3. Maths
  4. Level 7-8 Shapes - Pythagoras 02
Level 7-8 Shapes - Pythagoras 02
It's all about triangles!

Level 7-8 Shapes - Pythagoras 02

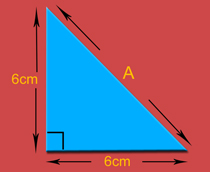
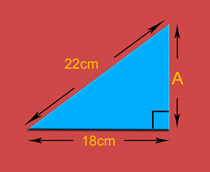
Use Pythagoras’ theorem to find missing sides in right-angled triangles. Practise squares, square roots, and checking triangles using a2 + b2 = c2.

Fascinating Fact:

Pythagoras was not just a mathematician; he studied music and found that harmonious notes follow simple ratios like 3:4:5, just like his famous right-angled triangles.

In KS3 Maths, Pythagoras’ theorem links the sides of a right-angled triangle: a2 + b2 = c2, where c is the hypotenuse (the longest side). You’ll use it to find missing lengths, rearrange to get square roots, and solve real problems like ladder lengths, diagonals of rectangles, and map distances.

Key Terms

  • Right-angled triangle: A triangle with one 90° angle.
  • Hypotenuse: The longest side in a right-angled triangle, opposite the right angle.
  • Pythagorean triple: Three whole numbers that fit a2 + b2 = c2, like 3, 4, 5 or 5, 12, 13.

Frequently Asked Questions (Click to see answers)

What is Pythagoras’ theorem in KS3?

Pythagoras’ theorem says that in a right-angled triangle, the sum of the squares of the shorter sides equals the square of the hypotenuse: a2 + b2 = c2.

How do I find a missing side using Pythagoras?

If you need the hypotenuse, use c = √(a2 + b2). If you need a shorter side, use a = √(c2 − b2) or b = √(c2 − a2).

How can I tell if three lengths make a right-angled triangle?

Square the two shorter lengths and add them. If the total equals the square of the longest length (a2 + b2 = c2), the triangle is right-angled.

Try These Related Quizzes

1 .
What is the length of the hypotenuse (A) in the triangle below?
16 cm
20 cm
24 cm
28 cm
162 + 122 = 400
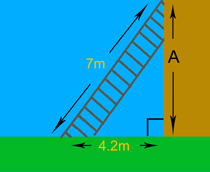
The square root of 400 is 20
2 .
What is the length of the hypotenuse (A) in the triangle below?
17.9 cm
24.1 cm
30.4 cm
36.8 cm
The answer is given here to 3 significant figures
3 .
What is the length of the hypotenuse (A) in the triangle below?
30.3 cm
32.1 cm
33.9 cm
36.7 cm
242 + 242 = 1,152
The square root of 1,152 is 33.9411....
4 .
What is the length of the hypotenuse (A) in the triangle below?
6.54 cm
8.49 cm
10.22 cm
12.44 cm
62 + 62 = 72
The square root of 72 is 8.4852....
5 .
What is the length of the hypotenuse (A) in the triangle below?
6.54 cm
8.49 cm
10.22 cm
12.44 cm
Well done if you spotted it is the same triangle as in question 4 but presented at a different rotation!
6 .
What is the length of the hypotenuse (A) in the triangle below?
11.5 cm
13.4 cm
15.3 cm
17.8cm
62 + 122 = 180
The square root of 180 is 13.416.....
7 .
What is the length of the side (A) in the triangle below?
4.7 cm
5.7 cm
6.7 cm
7.7 cm
62 + a2 = 92
36 + a2 = 81 so a2 = 45
The square root of 45 is 6.708....
8 .
What is the length of the side (A) in the triangle below?
9.8 cm
10.9 cm
12.6 cm
13.4 cm
182 + a2 = 222
324 + a2 = 484 so a2 = 160
The square root of 160 is 12.649...
9 .
The diagram below shows a ladder leaning against a vertical house wall. How far up the wall does the ladder reach?
4.4 m
4.8 m
5.2 m
5.6 m
4.22 + a2 = 72
17.64 + a2 = 49 so a2 = 31.36
The square root of 31.36 is 5.6
10 .
What is the diagonal of the rectangular swimming pool in the picture below?
10.98 m
11.05 m
11.18 m
11.76 m
Think of the diagonal as the hypotenuse of a right angled triangle
You can find more about this topic by visiting BBC Bitesize - Pythagoras

Author:  Frank Evans (Specialist 11 Plus Teacher and Tutor)
Maths Play this quiz again

Contact Details

Education Quizzes

Heron's Way, Wragg Marsh
Spalding
Lincolnshire
PE12 6HH
England

Email

admin@educationquizzes.com

Customer Service

Home Page Parents Students Tutors Teachers
Colour Filters Safe AI
Your Account

Here To Help

Contact Us Quiz List and Sitemap FAQs Links and Resources Blog

About Us

Our Team Testimonials Parent Reviews Terms and Conditions Privacy Policy

© Copyright 2016-2025 - Education Quizzes
Work Innovate Ltd - Design | Development | Marketing

We use cookies to enhance your experience on our website.

To comply with the e-Privacy directive, we need your consent - I agree - No thanks - Learn more